[동적 계획법 - Dynamic Programing] DP란?

DP란?

DP, Dynamic Programming(동적 계획법)은 무엇일까?
DP란, 하나의 큰 문제를 작은 문제로 나누어 해결하는 기법을 의미한다. 특정한 알고리즘을 지칭하는 것이 아니라, 기법 그 자체를 의미한다. 같은 DP로 문제를 풀어도 다른 알고리즘을 이용할 수도 있다는 것이다. 

DP가 무엇인지 처음 듣는 사람은 문제를 작은 문제로 나누어 해결하는 기법이 왜 Dynamic Programming이라 불리는 것일까, 하고 궁금증을 가질 수도 있다. 이에 대한 대답은 그저 '멋있어서'이다. Dynamic Programming이란 명칭을 고안한 Richard Bellman에 따르면 말이다. 

DP는 왜 중요할까?

백준, 코드포스 등 PS(Problem Solving) 사이트에서 문제를 풀다 보면 DP로 푸는 문제들을 심심찮게 볼 수 있다.
그러나 그 문제들 중 몇몇을 제외하면 DP 없이도 결과를 낼 수 있는 문제가 많다.
그렇다면 왜 DP로 문제를 푸는 것이고, 왜 중요할까?

피보나치 수 문제를 예로 들어보자. 
피보나치 수의 기본적인 형태는 f(n) = f(n-1) + f(n-2), n > 2 이다. 
이를 재귀함수로 나타내면 

int f(int n){
	if(n == 0 || n == 1) return 1;
    return f(n-1) + f(n-2);
}

이다. 여기서 문제가 발생한다. 재귀적으로 n번째 수를 구하기 위해 n번째보다 앞의 값을 구한다. 이 부분에 대해서는 문제가 없다. 
하지만 앞의 값을 여러 번 구한다는점에서 문제가 발생한다. n이 커질수록, 기하급수적으로 비효율적인 프로그램이 되는 것이다. 

그러나 한번 구한 값은 배열 등에 저장을 해두고 다시 필요하면 재귀를 돌릴 필요 없이 저장된 값을 불러오면 문제를 해결할 수 있다. 
재귀 함수만을 사용하면 점화식으로 문제를 푸는 것이지만, 메모이제이션까지 이용하여 DP, 문제를 작은 문제로 분해 후 해결하는 것이다. 

간단한 예를 들기 위해 피보나치를 언급했지만, 사실 이 문제는 단순히 단항식의 반복문으로 풀 수 있다. 
이제 DP의 조건을 알아보자. 

DP의 사용 조건

DP가 적용되기 위해서, 또는 문제풀이 기법이 DP라 부르기 위해서는 2가지 조건이 필요하다. 

• 겹치는 소문제 ( Overlapping Subproblems )
• 최적 부분 구조 ( Optimal Substructure )

첫 번째는 겹치는 소문제이다. 기본적으로 DP는 문제를 작은 문제로 나누고, 작은 문제의 결과를 재사용해서 원하는 결과를 도출하는 과정이다. 따라서 문제를 작은 문제를 나눴을 때 작은 문제들이 동일하게, 또는 비슷한 형태로 반복될 경우에 DP를 적용할 수 있다. 
만약 문제를 나눌 순 있어도, 중복되는 부분이 없어 각 소문제의 결과를 재사용할 수 없다면 DP를 적용하기 어렵다. 

다음은 최적 부분 구조이다. 소문제들의 최적 결과 값을 이용해 전체 문제의 최적 결과를 낼 수 있는 경우에 DP를 적용할 수 있다. 
자세하게 설명해보자면, 소문제에서 구한 최적의 결과가 전체 문제에서도 적용되며 이는 변하지 않을 때만 DP를 사용할 수 있다는 것이다. 
예를 들어 A에서 C로 가는 최단경로를 찾는 문제를 생각해보자. 

경로 1

경로 1이 주어진 경우에는 A-C 최단경로를 A-B, B-C 각각의 최단경로 소문제로 나눌 수 있다. 이때 각각의 최단경로는 AB2, BC2이며, 전체 문제에서의 최단경로도 AB2, BC2길이다. 이것이 작은 문제로 풀고 이를 전체 문제에 적용하는 것이다. 

경로 2

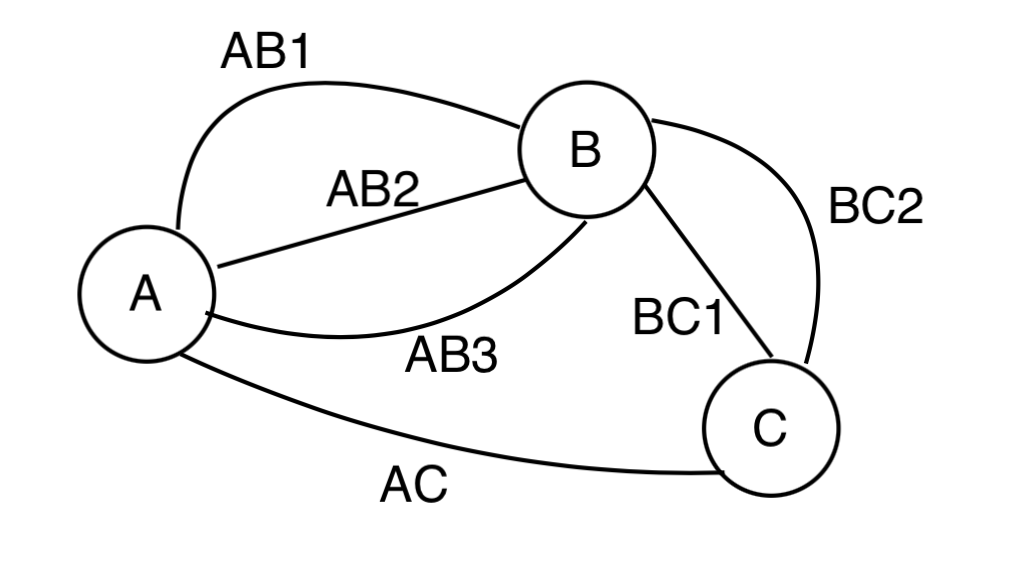
그러나 경로 2의 경우 A-B, B-C로 문제를 나누어 최단경로를 구해도, 전체 문제에서의 최단경로는 AC로 DP로 구하고자 한 것과 다르다. 
즉 이렇게 문제를 나누면 최적 부분 구조를 만족하지 않는 것이다. 

경로 2의 경우를 DP로 풀기 위해서는 소문제에 A-C경로도 포함하고 거리의 최솟값을 갱신하는 과정을 포함해야 한다. 

DP 적용하기

DP는 매우 많은 상황에서 적용 가능하다. 특히 어려운 문제는 침착하게 작은 문제로 나누어 DP를 적용하면 쉽게 풀리는 경우도 다수 있다. 
그렇다면 DP는 어떻게 적용해야 할까?

• 먼저, DP로 풀 수 있는 문제인지 확인해야 한다. 사실 이 처음 판별 과정이 제일 힘들다. DP로 풀 수 있는 것을 확인하면 문제는 반 정도 푼 것이나 다름없다. 확인하기 위해서는 앞서 소개한 조건들을 충족하는지를 확인하고, 어떻게 소문제로 나눌 수 있는지를 생각하면 된다. 
• 다음은 각 소문제들을 나누는 기준인 변수를 정하는 것이다. 피보나치 수의 경우엔 n번째의 n, 격자 관련 문제의 경우 행과 열 번호인 i, j 등이다. 
• 변수들을 정하면 이 변수들 간의 관계식, 즉 점화식을 찾는다. 피보나치 수를 다시 예로 들자면 f(n) = f(n-1) + f(n-2)가 있다.
• 마지막으로는 메모이제이션과 초기 조건이다. 비효율적인 재호출을 방지하기 위해 소문제의 결과를 저장해 두고, 소문제들의 결괏값 도출의 기반인 초기 조건을 구해둔다. 
• 앞선 단계들을 완료하면 이제 구현을 하고, 몇몇 값을 대입해보면서 정상적으로 작동하는지 확인한다. 

추가

DP를 적용하는 단계에서 구현을 할 때, 보통 두 가지 방법이 있다. 각각 Top-Down방식과 Botton-Up방식이다. 

• Botton-Up방식은 말 그대로 초기조건을 기반으로 차곡차곡 데이터를 쌓아가 큰 문제의 결과를 도출하는 과정이다. 보통 반복문을 사용한다. 예를 들어 메모이제이션을 위한 배열 dp[]가 있었다면, dp[0] 부터 차례로 값을 채운다. Bottom-Up에 한하여 이러한 값 채우기를 본 떠 메모이제이션을 Tabulation이라 부르기도 한다. 
• Top-Down방식은 주로 재귀함수를 사용하며 dp[n]값을 찾기 위한 재귀 함수의 호출이 dp[0](또는 초기 조건까지) 내려간 다음 결과들이 재귀 함수에 맞물리며 재활용되는 방식이다. 

필자는 Top-Down방식이 직관적으로 보여 이 방식을 선호한다. DP로 문제를 풀 때 Botton-Up방식으로는 거의 푼 기억이 없다. 
하지만 두 방식 모두 좋은 방법이며, 각자의 취향에 따라 코드를 써내려가면 된다. 

분할정복도 DP와 함께 자주 언급된다. 두 기법은 모두 문제를 소문제로 나누어 해결한다는 공통점이 있지만, 분할정복은 하위 문제에서 중복이 일어나지 않는 방면, DP는 하위 문제에서 중복이 일어난다는 차이점이 있다.